Nei sistemi dinamici è rilevante la complementarietà ricursiva tra forma (o struttura) e processo. La forma del sistema e/o la struttura-configurazione dei suoi elementi dinamici determina quali tipi di processo possono avvenire, viceversa i processi di sistema sono determinati dalla struttura e dalla dinamica dei componenti. Particolarmente in biologia il processo che porta ad una determinata forma o struttura è denominato morfogenesi, la genesi (creazione) della forma, dal greco morfè.
Nell'ambito di quella che oggi è la moderna teoria del caos René Thom propose in modo pionieristico negli anni 50 e 60 una sofisticata teoria generale della morfogenesi conosciuta come teoria delle catastrofi, una branca della teoria delle biforcazioni nello studio dei sistemi dinamici e un caso particolare della teoria delle singolarità globale.
Un esempio tra i più semplici di sistema catastrofico è quello illustrato in figura, dove una palla è libera di muoversi sotto l'effetto della gravità in un contenitore con due buche di potenziale gravitazionale.
Il sistema ha due punti di equilibrio stabile, sul fondo delle buche, e uno instabile in cima alla separazione tra le due buche e può essere completamente descritto in uno spazio degli stati, dove le variabili di stato si possono scegliere come l'angolo di tilt del contenitore rispetto alla posizione orrizzontale (variabile di controllo) e la posizione della palla. Il sistema è quindi modellizzabile come un sistema di tipo input/output, dove la posizione della palla (l'output) dipende dalla variabile di controllo (l'input).
Una catastrofe è definita come un punto della relazione output/input dove una variazione minima dell'input provoca una grande variazione dell'output; corrispondentemente la variazione della relazione output/input presenta una singolarità.
"La teoria delle catastrofi ha un programma che è facile da esporre: si tratta di spiegare le forme naturali. Quando posiamo il nostro sguardo sul mondo, constatiamo che l’universo non è un caos, che è diviso in forme relativamente distinte, ben separate le une dalle altre.
E’ più simile all’ordine di un cosmo che non un caos. Da questo punto di vista, ciò che la teoria delle catastrofi tenta di fare è di esplicare l’origine e la successione delle forme naturali così come le percepiamo nel mondo che ci circonda. Questo punto di vista della teoria delle catastrofi è abbastanza nuovo, nel senso che essa si propone di edificare una teoria che spieghi la genesi delle forme indipendentemente dal substrato materiale che le compone. Questo ha qualcosa di un po’ paradossale, perchè sappiamo per certo che una nuvola non ha la stessa consistenza di un blocco di marmo, e che di conseguenza la permanenza delle forme è strettamente legata alla natura del loro substrato. Non ci sono dubbi sul fatto che la natura del substrato abbia effettivamente un ruolo di primo piano nel determinare il carattere più o meno permanente, o al contrario più o meno transitorio, di una forma. Ma, ciononostante, la teoria delle catastrofi adotta un punto di vista risolutamente indipendente dal substrato. In altre parole, ci si pone in un’ottica per cui c’è qualcosa come un etere soggiacente che riempie
tutto lo spazio. Una materia prima, avrebbe detto Aristotele. Questa materia prima è sottomessa a delle sollecitazioni che le fanno adottare questo o quell’altro tipo di materia. Quello che la teoria delle catastrofi propone sono gli schemi generali che permettono di spiegare la genesi delle forme.
Facciamo l’esempio del piano della scrivania, che è qui davanti a me: abbiamo uno spigolo che separa la superficie orizzontale della scrivania dalla parete verticale. Questo spigolo per me è un luogo di catastrofe, perchè separa due superfici che hanno delle funzioni e degli orientamenti diversi. La natura del substrato è evidentemente la stessa: dell’aria da una parte e del legno dall’altra. Ma se si vuole risalire all’origine delle forme, ci si renderà conto che questo spigolo trae origine dal fatto che l’asse di legno che costituisce la scrivania è stata inizialmente segata da una sega, diciamo metallica, il cui disco ha tracciato una linea di contorno nel legno dell’asse. Ed è il conflitto fra l’acciaio della sega e la materia legno che ha generato la forma. La teoria delle catastrofi, se volete, ritorna alla vecchia idea eraclitea che il conflitto è il padre di tutte le cose. Qualsiasi forma deve la sua origine ad un conflitto."
Nell'ambito di quella che oggi è la moderna teoria del caos René Thom propose in modo pionieristico negli anni 50 e 60 una sofisticata teoria generale della morfogenesi conosciuta come teoria delle catastrofi, una branca della teoria delle biforcazioni nello studio dei sistemi dinamici e un caso particolare della teoria delle singolarità globale.
Il libro di Thom fu commentato da alcuni autori come "un enigma sia per la forma che per il contenuto. Era largamente inaccessibile alla comunità matematica perchè scritto nel linguaggio dei biologi, e inaccessibile alla comunità dei biologi per la presentazione di una serie di concetti matematici di topologia differenziale che sembravano profondi e misteriosi."
La teoria di Thom fu ulteriormente sviluppata nelle sue possibili applicazioni e resa conosciuta negli anni 70 dal lavoro di Christopher Zeeman e successivamente estesa da Vladimir Arnol'd. Thom ricevette nel 1958 la Fields Medal, l'analogo del premio Nobel nell'ambito della matematica, per i suoi lavori di topologia differenziale.
Un esempio tra i più semplici di sistema catastrofico è quello illustrato in figura, dove una palla è libera di muoversi sotto l'effetto della gravità in un contenitore con due buche di potenziale gravitazionale.
Una catastrofe è definita come un punto della relazione output/input dove una variazione minima dell'input provoca una grande variazione dell'output; corrispondentemente la variazione della relazione output/input presenta una singolarità.
Nel sistema in esempio ruotando l'angolo di tilt in senso orario o antiorario si hanno due catastrofi simmetriche appena oltre le posizioni 2 e 6, dove la palla passa da una buca all'altra.
Questo semplice sistema illustra tutti i punti cruciali della teoria: per la maggior parte dei valori della variabile di controllo non succede nulla, la posizione rimane praticamente invariata; per i valori critici la posizione cambia drasticamente valore in modo non-lineare e corrispondentemente il sistema palla più contenitore cambia radicalmente topologia/forma passando la palla da una buca all'altra - la massima variazione possibile di struttura per questo sistema. E' da notare che, oltre alla particolare configurazione, deve esistere un meccanismo che ne regoli la dinamica, in questo caso la forza di gravità verso il basso, e inoltre la variazione considerata dello spazio degli stati deve essere limitata, o locale - oltre un certo valore della variabile di controllo il sistema ha una catastrofe totale irreversibile, cioè la palla esce dal contenitore, trasformandolo in uno completamente diverso.
Nell'esempio il sistema - pur esibendo due punti di catastrofe - è reversibile: muovendo avanti e indietro la variabile di controllo lo stato del sistema si porta nei due stati di equilibrio attraverso le due catastrofi. Altri sistemi possono essere irreversibili, ad esempio sistemi fisici di cui si solleciti l'elasticità: se si piega una forchetta con una certa forza entro i limiti elastici del materiale e poi si annulla questa torna alla forma originaria ma oltre un dato limite di elasticità diventa piegata in modo irreversibile, ed oltre ad un ulteriore limite di rottura si spezza in due parti, una vera e propria catastrofe totale irreversibile che modifica la morfologia del "sistema forchetta" da un'unico pezzo a due.
La raffigurazione in 2D di un sistema con una variabile di controllo e una di stato è, per esempio:
.JPG)
dove vi sono due punti di catastrofe in cui per una minima variazione della variabile di controllo si hanno ampie variazioni di quella di stato, e si presume una corrispondente variazione della configurazione del sistema.
Una rappresentazione generica in 3D per due variabili di controllo e una di stato è del tipo:
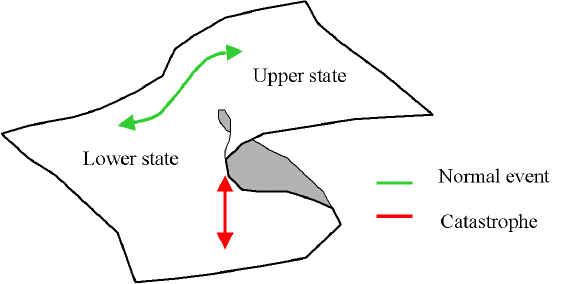
rappresentabile come un sistema dinamico con due input e un output. Il sistema ha due stati, ad esempio se il sistema rappresenta un gas/liquido e la variabile di stato è la densità e quelle di controllo temperatura e pressione lo stato inferiore rappresenta la fase gassosa del sistema e quella superiore la fase liquida e la traiettoria in verde rappresenta l'usuale transizione di fase da liquido a gas e viceversa.
La superficie di stato (o di equilibrio) può non presentare singolarità, cioè è "liscia" in ogni suo punto (come nel percorso verde precedente), oppure come in figura avere un "ripiegamento" topologico della sua struttura, che presenta una catastrofe di stato quando le due variabili di controllo la percorrono, come nel caso rosso della figura precedente o quello del percorso A in quella seguente:
Il comportamento del sistema nella parte catastrofica della superficie di stato dipende dal percorso:
Nel percorso A trasversale alla singolarità catastrofica in 2D si presenta un tipo di catastrofe ad S, mentre longitudinalmente (perpendicolare al percorso A) si trova una biforcazione.
La proiezione della singolarità sul piano della variabili di controllo, detta insieme di biforcazione, è denominata - in questo caso - cuspide e presenta un punto singolare.
Quando un punto di catastrofe è presente in una superficie di stato vi sono diversi fenomeni che posso avere luogo, detti flags della catastrofe:
In una catastrofe a cuspide come quella rappresentata vi sono cinque flags "classici" che avvengono quandi si ha un cambiamento qualitativo/strutturale del sistema: modalità, salto improvviso (sudden jump), inaccessibilità, sensibilità e isteresi. I rimanenti tre, come i precedenti, avvengono quando si ha un cambiamento strutturale ma possono essere osservati anche prima del cambiamento e sono denominati flags "diagnostici": divergenza della risposta lineare, dilatazione del tempo e varianza anomala. Ad ognuno di questi flags corrisponde un diverso comportamento catastrofico del sistema.
Il risultato maggiore di Thom, conosciuto come teorema di classificazione, attesta che per un numero di variabili di controllo minore o uguale a 4 vi possono essere solo sette tipi di singolarità, denominate da Thom catastrofi elementari:
La struttura (o la proiezione) della superficie di stato in 3D per due variabili di controllo per le prime cinque catastrofi elementari è:
Le singolarità delle superfici di stato locali dei sistemi dinamici non sono quindi arbitrarie ma devono necessariamente, se esistono, appartenere ad una delle sette catastrofi elementari definite dal teorema di classificazione di Thom.
Di queste quella più utilizzata per modellare sistemi reali è la cuspide, sia perchè è la più semplice sia perchè è fra le uniche due riproducibili interamente in uno spazio 3D. Un esempio fisico misurabile riprodotto da questa catastrofe elementare è il punto critico nella transizione di fase tra un liquido e un gas nelle variabili di controllo temperatura e pressione e in quella di stato densità:
Nelle condizioni di un fluido/gas perfetto la superficie di equilibrio non presenta discontinuità e il passaggio da liquido a gas (ebollizione) e da gas a liquido (condensazione) avviene alla stessa temperatura a parità di pressione.In un sistema gas/liquido reale possono accadere le condizioni in cui un liquido sia portato ad un temperatura maggiore di quella di ebollizione e un gas ad una inferiore a quella di condensazione (vapore e liquido sovrassaturo). In questo stato il sistema è metastabile e può effettuare un sudden crash verso l'una o l'altra condizione stabile di equilibrio.
L'applicazione della teoria delle catastrofi a sistemi reali è stata perseguita basandosi sul fatto che sia le variabili coinvolte sia il teorema di classificazione sono del tutto generali e la loro teoria è completa, e quindi applicabile in linea di principio a ogni tipo di sistema. La difficoltà di applicazione consiste nel fatto che se il sistema non è formalizzabile o misurabile la teoria rimane qualitativa, un'utile rappresentazione o metafora per spiegare la dinamica del sistema, ma non utilizzabile per predizioni quantitative. Nella sua review del 1976 su Scientific American Zeeman porta una serie di esempi di applicazione in settori molto diversi quali l'etologia, la psicologia, l'economia, la politica della guerra e i disturbi mentali o di comportamento quali l'anoressia nervosa.
Ad esempio Zeeman riporta un'applicazione alla politica della guerra modellata su una catastrofe elementare di tipo a farfalla:
La catastrofe a farfalla modella il comportamento su quattro variabili di controllo e in questo caso, per poterla rappresentare in 3D, solo due sono utilizzate - costo e minaccia - mentre le altre due sono assunte costanti. La variabile di stato è il risultato che si ottiene e varia dall'attacco militare alla resa alla negoziazione.
Un altro esempio è un modello economico del comportamento di borsa modellato da una catastrofe a cuspide:
nel quale le variabili di controllo sono l'eccesso di domanda e la speculazione e la variabile di stato è tasso di cambiamento dell'indice dei prezzi. I due livelli della superficie sono quelli comunemente definiti come bull e bear markets (rialziasta e ribassista). Il crash tramite un flag di sudden jump nella catastrofe a cuspide tra alti e bassi valori di mercato è provocato quando con alti indici di mercato e un'alta percentale di speculatori nel bull market un qualsiasi evento riduca la domanda e faccia precipitare gli indici sui valori bassi del bear market.
E' evidente come questo esempi di aplicazione della teoria delle catastrofi siano rappresentativi ma difficilmente quantitativi. L'utilizzo soprattutto della catastrofe a cuspide è stato invocato per rappresentare ogni tipo di "sistema" e di "stati" in modo del tutto metaforico, ad esempio:
questa cuspide vorrebbe rappresentare genericamente il comportamento ottenuto su vari percorsi di "ottimismo" e "pessimismo", passando attraverso stati di disastro, declino, neutralità, miglioramento e utopici con un possibile crash catastrofico che da elevati comportamenti utopici portano a un disastro.
Il senso della teoria secondo Thom può essere riassunto in questa risposta da un'intervista del 1988:
Nell'esempio il sistema - pur esibendo due punti di catastrofe - è reversibile: muovendo avanti e indietro la variabile di controllo lo stato del sistema si porta nei due stati di equilibrio attraverso le due catastrofi. Altri sistemi possono essere irreversibili, ad esempio sistemi fisici di cui si solleciti l'elasticità: se si piega una forchetta con una certa forza entro i limiti elastici del materiale e poi si annulla questa torna alla forma originaria ma oltre un dato limite di elasticità diventa piegata in modo irreversibile, ed oltre ad un ulteriore limite di rottura si spezza in due parti, una vera e propria catastrofe totale irreversibile che modifica la morfologia del "sistema forchetta" da un'unico pezzo a due.
La raffigurazione in 2D di un sistema con una variabile di controllo e una di stato è, per esempio:
.JPG)
dove vi sono due punti di catastrofe in cui per una minima variazione della variabile di controllo si hanno ampie variazioni di quella di stato, e si presume una corrispondente variazione della configurazione del sistema.
Una rappresentazione generica in 3D per due variabili di controllo e una di stato è del tipo:
rappresentabile come un sistema dinamico con due input e un output. Il sistema ha due stati, ad esempio se il sistema rappresenta un gas/liquido e la variabile di stato è la densità e quelle di controllo temperatura e pressione lo stato inferiore rappresenta la fase gassosa del sistema e quella superiore la fase liquida e la traiettoria in verde rappresenta l'usuale transizione di fase da liquido a gas e viceversa.
La superficie di stato (o di equilibrio) può non presentare singolarità, cioè è "liscia" in ogni suo punto (come nel percorso verde precedente), oppure come in figura avere un "ripiegamento" topologico della sua struttura, che presenta una catastrofe di stato quando le due variabili di controllo la percorrono, come nel caso rosso della figura precedente o quello del percorso A in quella seguente:
Il comportamento del sistema nella parte catastrofica della superficie di stato dipende dal percorso:
Nel percorso A trasversale alla singolarità catastrofica in 2D si presenta un tipo di catastrofe ad S, mentre longitudinalmente (perpendicolare al percorso A) si trova una biforcazione.
La proiezione della singolarità sul piano della variabili di controllo, detta insieme di biforcazione, è denominata - in questo caso - cuspide e presenta un punto singolare.
 |
| Manoscritto originario di Thom per una biforcazione a cuspide in 2D |
Il risultato maggiore di Thom, conosciuto come teorema di classificazione, attesta che per un numero di variabili di controllo minore o uguale a 4 vi possono essere solo sette tipi di singolarità, denominate da Thom catastrofi elementari:
La struttura (o la proiezione) della superficie di stato in 3D per due variabili di controllo per le prime cinque catastrofi elementari è:
Le singolarità delle superfici di stato locali dei sistemi dinamici non sono quindi arbitrarie ma devono necessariamente, se esistono, appartenere ad una delle sette catastrofi elementari definite dal teorema di classificazione di Thom.
Di queste quella più utilizzata per modellare sistemi reali è la cuspide, sia perchè è la più semplice sia perchè è fra le uniche due riproducibili interamente in uno spazio 3D. Un esempio fisico misurabile riprodotto da questa catastrofe elementare è il punto critico nella transizione di fase tra un liquido e un gas nelle variabili di controllo temperatura e pressione e in quella di stato densità:
Nelle condizioni di un fluido/gas perfetto la superficie di equilibrio non presenta discontinuità e il passaggio da liquido a gas (ebollizione) e da gas a liquido (condensazione) avviene alla stessa temperatura a parità di pressione.In un sistema gas/liquido reale possono accadere le condizioni in cui un liquido sia portato ad un temperatura maggiore di quella di ebollizione e un gas ad una inferiore a quella di condensazione (vapore e liquido sovrassaturo). In questo stato il sistema è metastabile e può effettuare un sudden crash verso l'una o l'altra condizione stabile di equilibrio.
L'applicazione della teoria delle catastrofi a sistemi reali è stata perseguita basandosi sul fatto che sia le variabili coinvolte sia il teorema di classificazione sono del tutto generali e la loro teoria è completa, e quindi applicabile in linea di principio a ogni tipo di sistema. La difficoltà di applicazione consiste nel fatto che se il sistema non è formalizzabile o misurabile la teoria rimane qualitativa, un'utile rappresentazione o metafora per spiegare la dinamica del sistema, ma non utilizzabile per predizioni quantitative. Nella sua review del 1976 su Scientific American Zeeman porta una serie di esempi di applicazione in settori molto diversi quali l'etologia, la psicologia, l'economia, la politica della guerra e i disturbi mentali o di comportamento quali l'anoressia nervosa.
Ad esempio Zeeman riporta un'applicazione alla politica della guerra modellata su una catastrofe elementare di tipo a farfalla:
La catastrofe a farfalla modella il comportamento su quattro variabili di controllo e in questo caso, per poterla rappresentare in 3D, solo due sono utilizzate - costo e minaccia - mentre le altre due sono assunte costanti. La variabile di stato è il risultato che si ottiene e varia dall'attacco militare alla resa alla negoziazione.
Un altro esempio è un modello economico del comportamento di borsa modellato da una catastrofe a cuspide:
nel quale le variabili di controllo sono l'eccesso di domanda e la speculazione e la variabile di stato è tasso di cambiamento dell'indice dei prezzi. I due livelli della superficie sono quelli comunemente definiti come bull e bear markets (rialziasta e ribassista). Il crash tramite un flag di sudden jump nella catastrofe a cuspide tra alti e bassi valori di mercato è provocato quando con alti indici di mercato e un'alta percentale di speculatori nel bull market un qualsiasi evento riduca la domanda e faccia precipitare gli indici sui valori bassi del bear market.
E' evidente come questo esempi di aplicazione della teoria delle catastrofi siano rappresentativi ma difficilmente quantitativi. L'utilizzo soprattutto della catastrofe a cuspide è stato invocato per rappresentare ogni tipo di "sistema" e di "stati" in modo del tutto metaforico, ad esempio:
questa cuspide vorrebbe rappresentare genericamente il comportamento ottenuto su vari percorsi di "ottimismo" e "pessimismo", passando attraverso stati di disastro, declino, neutralità, miglioramento e utopici con un possibile crash catastrofico che da elevati comportamenti utopici portano a un disastro.
Il senso della teoria secondo Thom può essere riassunto in questa risposta da un'intervista del 1988:
"La teoria delle catastrofi ha un programma che è facile da esporre: si tratta di spiegare le forme naturali. Quando posiamo il nostro sguardo sul mondo, constatiamo che l’universo non è un caos, che è diviso in forme relativamente distinte, ben separate le une dalle altre.
E’ più simile all’ordine di un cosmo che non un caos. Da questo punto di vista, ciò che la teoria delle catastrofi tenta di fare è di esplicare l’origine e la successione delle forme naturali così come le percepiamo nel mondo che ci circonda. Questo punto di vista della teoria delle catastrofi è abbastanza nuovo, nel senso che essa si propone di edificare una teoria che spieghi la genesi delle forme indipendentemente dal substrato materiale che le compone. Questo ha qualcosa di un po’ paradossale, perchè sappiamo per certo che una nuvola non ha la stessa consistenza di un blocco di marmo, e che di conseguenza la permanenza delle forme è strettamente legata alla natura del loro substrato. Non ci sono dubbi sul fatto che la natura del substrato abbia effettivamente un ruolo di primo piano nel determinare il carattere più o meno permanente, o al contrario più o meno transitorio, di una forma. Ma, ciononostante, la teoria delle catastrofi adotta un punto di vista risolutamente indipendente dal substrato. In altre parole, ci si pone in un’ottica per cui c’è qualcosa come un etere soggiacente che riempie
tutto lo spazio. Una materia prima, avrebbe detto Aristotele. Questa materia prima è sottomessa a delle sollecitazioni che le fanno adottare questo o quell’altro tipo di materia. Quello che la teoria delle catastrofi propone sono gli schemi generali che permettono di spiegare la genesi delle forme.
Facciamo l’esempio del piano della scrivania, che è qui davanti a me: abbiamo uno spigolo che separa la superficie orizzontale della scrivania dalla parete verticale. Questo spigolo per me è un luogo di catastrofe, perchè separa due superfici che hanno delle funzioni e degli orientamenti diversi. La natura del substrato è evidentemente la stessa: dell’aria da una parte e del legno dall’altra. Ma se si vuole risalire all’origine delle forme, ci si renderà conto che questo spigolo trae origine dal fatto che l’asse di legno che costituisce la scrivania è stata inizialmente segata da una sega, diciamo metallica, il cui disco ha tracciato una linea di contorno nel legno dell’asse. Ed è il conflitto fra l’acciaio della sega e la materia legno che ha generato la forma. La teoria delle catastrofi, se volete, ritorna alla vecchia idea eraclitea che il conflitto è il padre di tutte le cose. Qualsiasi forma deve la sua origine ad un conflitto."
 |
| Salvador Dali, Enlevement topologique d’Europe. Hommage à René Thom, 1983 |
Nessun commento:
Posta un commento