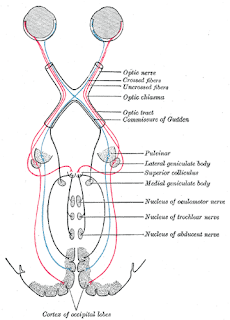
La situazione del sistema visivo nel cervello, ovvero che il sistema è organizzato in forma reticolare, e vi è una convergenza o coerenza di tutte le parti in questione, non è specifica del sistema in questione ma è generalizzabile a tutte le aree del cervello ed in generale a tutto il sistema nervoso: il flusso di processo/informazione avviene in una rete globale a molteplici interconnessioni che funziona in ogni istante generando uno stato di coerenza interna secondo un processo cooperativo.
Il punto centrale per la descrizione di un tale insieme di processi non è più stabilire il flusso di informazioni, cosa praticamente impossibile e anche inutile, ma le modalità specifiche in cui gli stati di coerenza interna si producono nell'ambito di questa rete che definisce se-stessa.
Questo richiede un cambiamento dal principio generale paradigmatico per descrivere i sistemi utilizzando lo schema stimolo/risposta, input/output, etc., caratteristico dei sistemi eteronomi.
Tale schema va bene quando si tratta con computer o circuiti di controllo o sistemi cibernetici, ma non quando si ha a che fare con sistemi complessi come il sistema nervoso.
Maturana e Varela hanno definito un concetto chiave (solo apparentemente tautologico) per questi ultimi come Chiusura Operazionale:
Maturana e Varela hanno definito un concetto chiave (solo apparentemente tautologico) per questi ultimi come Chiusura Operazionale:
le conseguenze delle operazioni del sistema
sono le operazioni del sistema
sono le operazioni del sistema
dove chiusura (closure) non è isolamento (closeness). La Chiusura Operazionale definisce degli autocomportamenti (eigenbehaviors) in cui le operazioni di un sistema complesso, costituito da elementi interconnessi, hanno come risultato un'operazione che cade ancora entro i confini del sistema stesso e della propria dinamica interna.
La chiusura si riferisce al fatto che il risultato di un’operazione cade ancora entro i confini del sistema stesso, questo non significa che il sistema non abbia interazioni con l’ambiente esterno, dato che - come tutti i sistemi viventi, è un sistema aperto: il sistema è chiuso organizzativamente ma aperto per quanto riguarda l'energia e lo scambio con l'ambiente. La Chiusura Operazionale definisce i punti di stabilità e di autonomia, ovvero dove le relazioni e interazioni che definiscono il sistema nel suo complesso sono determinate solamente dal sistema stesso, ed infine definisce l'omeostasi del sistema, una condizione di interazione complementare stabilità/cambiamento che ha come conseguenza la persistenza del sistema a seguito di cambiamenti: per poter essere sempre se stesso il sistema deve continuamente cambiare, e contemporaneamente per poter cambiare deve rimanere se stesso.
Un esempio di chiusura operazionale di un sistema complesso è quello tra sistema senso-motorio e sistema nervoso:
Lo stesso esempio vale per lo schema di una cellula:

La rete metabolica interna alla cellula produce una membrana cellulare tale che permette alla rete metabolica di produrre i metaboliti che la costituiscono, e così via. Attraverso la membrana cellulare vi è poi l'interscambio di energia, molecole etc. tipiche dei sistemi aperti. Il sistema ha evidenti caratteristiche di chiusura operazionale, stabilità, autonomia e omeostasi.
In generale la chiusura operazionale come processo circolare ricursivo nei sistemi viventi lega un sistema autonomo che genera una rete di processi che produce dei componenti del sistema che a loro volta determinano la chiusura/autonomia del sistema, e così via:
Maturana e Varela hanno simboleggiato schematicamente la struttura di un qualsiasi sistema vivente come:
dove la parte di chiusura circolare che definisce, ed è a sua volta definita, dall'organizzazione del sistema vivente scambia interazioni con l'ambiente come un sistema aperto.
La tabella seguente riassume le caratteristiche dei sistemi eteronomi e autonomi:
sistemi eteronomi sistemi autonomi
logica delle operazioni corrispondenza coerenza
tipo di organizzazione input/output chiusura operazionale
modo di interazione istruttivo-rappresentazionale produzione di un mondo
Il concetto di chiusura operazionale, definito come il fatto che un sistema ha stati di coerenza, - e si potrebbe dire di esistenza - nel caso in cui le operazioni compiute del sistema ricadano entro il dominio del sistema stesso, è del tutto generale.
Al livello 0 e 1 fisico-chimico, dove è disponibile un sistema formale, esso è rappresentato da una classe fondamentale di equazioni dette equazioni agli autovalori, nella forma
Hf=af
dove H è un operatore funzionale, f delle funzioni definite su uno spazio funzionale S(f) e gli a sono in generale dei numeri reali.
Se l'equazione, dato un determinato operatore H, e specificate le condizioni al contorno, ammette delle soluzioni fi e ai, con i un indice discreto o continuo in dipendenza delle condizioni al contorno, allora queste vengono dette autofunzioni (eigenfunctions) e autovalori (eigenvalues) dell'equazione.
L'equazione esprime interamente il concetto di chiusura operazionale, nel senso che fatta un'operazione H su una funzione fi il risultato è ancora la funzione fi a meno di un numero ai, ovvero l'operazione ricade sempre nello spazio funzionale S(f).
In fisica alcune delle equazioni più importanti sono di questa forma, in particolare (per gli stati stazionari - ovvero invarianti nel tempo) le equazioni del moto di Newton della meccanica classica, espresse in forma hamiltoniana, e quelle della meccanica quantistica nelle due rappresentazioni duali funzione d'onda/particella espresse nel primo caso dall'equazione di Schrödinger e nel secondo dall'equazione di Heisenberg, dove H è l'operatore hamiltoniano associato all'energia del sistema.
Le soluzioni in entrambe le rappresentazioni forniscono le funzioni d'onda del sistema e gli autovalori dell'energia, ad esempio nel caso del sistema fisico-chimico più semplice, quello dell'atomo di idrogeno, le autofunzioni d'onda sono del tipo:
mentre gli autovalori dell'energia forniscono la serie di livelli quantici discreti possibili per l'elettrone:
Allo stesso modo la soluzione delle equazioni agli autovalori dell'energia per elementi superiori, molecole e catene di molecole con il metodo degli orbitali atomici pongono le basi per il legame chimico e quindi per l'esistenza di ogni composto chimico.
Un'altra classe fondamentale è quella in cui gli operatori H sono lineari, e definiscono quindi un sistema lineare; in questo caso ogni funzione f è un'autofunzione e, a seconda che gli autovalori siano maggiori o minori di 1, si hanno caratteristiche di amplificazione o attenuazione.
Un'altra classe fondamentale è quella in cui gli operatori H sono lineari, e definiscono quindi un sistema lineare; in questo caso ogni funzione f è un'autofunzione e, a seconda che gli autovalori siano maggiori o minori di 1, si hanno caratteristiche di amplificazione o attenuazione.
Ai livelli superiori al 2-3 biologico/organismo il concetto di chiusura operazionale continua ad essere significativo come linea guida per definire o stabilire quali siano gli stati stabili di sistema.
Vi possono essere casi di meta-chiusura operazionale; un esempio tipico di Von Foerster è l'accoppiamento tra sistema nervoso e sistema endocrino:

Sia il sistema nervoso che quello endocrino sono a chiusura operazionale, rappresentata da cerchi chiusi, ed interagiscono tra di loro, in particolare l'endocrino stabilizza il nervoso e viceversa. Il sistema risultante è rappresentabile in modo tridimensionale da un toro, dove gli anelli longitudinali rappresentano un sistema e quelli trasversali l'altro. L'effetto risultante è quello di meta-regolazione, ovvero una regolazione della regolazione.
La trattazione generale della chiusura operazionale come limite di operazioni ricursive che ricadono sullo stesso dominio è stata sviluppata da Heinz Von Foerster nel seguente modo:
ammettiamo di avere una variabile x0: x0 ha un carattere del tutto generale, può essere un funzione, un valore numerico, una disposizione (liste di numeri, vettori, configurazioni geometriche), comportamenti descritti da funzioni, comportamenti descritti da proposizioni etc. Definiamo un'operazione su x0 simboleggiata da Op. Op può essere un operatore, un funzionale, un algoritmo etc. tale che applicato a x0 lo traforma in x1:
applicando successivamente l'operazione Op si ha
x1=Op(x0)
x2=Op(Op(x1))
......
xn=Op(n)(x0)
e ripetendo infinite volte l'applicazione di Op:
x∞=Op(∞)(x0)
ovvero
in quest'ultima espressione si nota che la variabile iniziale x0 è scomparsa, e che ogni sequenza infinita di Op può essere sostituita da Op(∞):
x∞=Op(x∞)
x∞=Op(Op(x∞))
x∞=Op(Op(Op(x∞)))
...
se questo sistema di equazioni ha delle soluzioni del tipo Ei=x∞i allora essi vengono detti autovalori, autooperatori, autoalgoritmi, autocomportamenti etc.
La chiusura operazionale è espressa quindi come limite di un processo ricorsivo di applicazioni di Op:
lim (n→∞) Op(n) = OP →
↑←↓
ed in particolare l'operatore Op implica i propri autovalori Ei, ed è da questi implicato; operatori e autovalori sono complementari:
Op↔Ei
inoltre, poichè gli Ei si autoproducono, attraverso gli Op(n) ad essi complementari, essi sono autoriflessivi.
Alcuni esempi portati da Von Foerster sono ad esempio l'operatore H=SQRT, la radice quadrata di un numero; partendo da qualsiasi numero reale positivo x0 ed applicando in successione infinite volte l'operazione SQRT si ha come autovalore x∞=1 e SQRT(1)=1 è un autovalore.
Un altro esempio è la frase (in italiano):
QUESTA FRASE HA ... LETTERE
dove al posto di ... si deve sostituire un numero in lettere che renda vera la frase; in questo caso vi sono due autovalori ad esempio VENTOTTO. Se si modifica la frase si possono avere più autovalori, uno o nessuno. In senso ontologico la frase esiste, ovvero diventa logicamente vera, solo per i suoi autovalori, altrimenti è falsa.
Nel caso dei livelli 2-3 studiati da Maturana e Varela la chiusura operazionale delle operazioni del sistema Op diventa:
ORG →
↑ ← ↓
ovvero la chiusura definisce l'organizzazione del sistema e viceversa l'organizzazione definisce la sua chiusura.